Persamaan Trigonometri Matematika Peminatan Kelas 11
Selamat datang di matematikakubro.blogspot.com gaes. Kali ini kita akan membahas tentang persamaan trigonometri. Persamaan trigonometri mempunyai beberapa bentuk. Ada yang sekedar menitikberatkan kepada hafalan sudut, ada yang mengkombinasikan dengan aturan kuadran, ada juga yang menggunakan bentuk persamaan kuadrat juga lho.
Disini persamaan trigonometri akan kita bagi menjadi beberapa bentuk. Antara lain
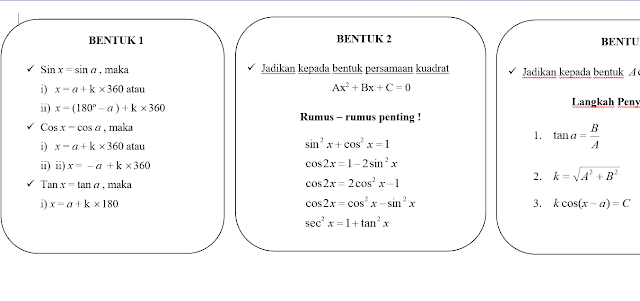
Bentuk 1
Persamaan Trigonometri bentuk 1 merupakan persamaan trigonometri yang paling sederhana.
ü Sin x = sin a , maka
i)
x = a + k x 360 atau
ii)
x = (180o – a ) + k x 360
ü Cos x = cos a , maka
i)
x = a + k x 360 atau
ii)
ii)
x =
– a + k x 360
ü Tan x = tan a , maka
i) x = a
+ k x 180
Perhatikan contoh berikut untuk lebih memahaminya !
1. Tentukan nilai x untuk sin x = 0,5 dengan 0 < x < 360
Untuk menjawab soal ini kita harus mengetahui sin berapa yang hasilnya setengah ?
yaitu sin 30. Namun kita juga harus melihat intervalnya. Disana tertulis 0 < x < 360 artinya kita harus cek apakah hanya sin 30 saja yang hasilnya 0,5 tentu tidak. Karena sin 150 juga hasilnya 0,5.
Artinya HP = {30, 150}
Kalau kalian bingung dengan cara itu silahkan amati cara dibawah ini
sin x = 0,5
sin x = sin 30
x = 30
i) x = 30 + k x 360
untuk k = 0 maka x = 30 + 0 x 360 sehingga x = 30
untuk k =1 maka x = 30 + 1 x 360 sehingga x = 390 (Tidak Memenuhi karena diluar interval)
ii) x = (180 - 30) + k x 360 atau x = 150 + k x 360
untuk k = 0 maka x = 150 + 0 x 360 sehingga x = 150
untuk k = 1 maka x = 150 + 1 x 360 sehingga x = 510 (Tidak Memenuhi karena diluar interval)
Jadi Himpunan penyelesainnya adalah HP = {30, 150}
2. Tentukan nilai x untuk cos 2x = 1 dengan 0 < x < 360
Untuk menjawab soal ini kita harus mengetahui cos berapa yang hasilnya adalah 1 ?
Yaitu cos 0. Apakah hanya itu ? tentu tidak. Cos 360 juga hasilnya 1. Apakah hanya itu ? tentu tidak karena cos 720 juga hasilnya adaalh 1.
Nah setelah itu kita hitung satu per satu namun kita lihat intervalnya adalah 0 < x < 360 artinya kita harus mencari nilai x yang ada dalam interval tersebut
cos 2x = cos 0
2x = 0
x = 0/2
x = 0
cos 2x = cos 360
2x = 360
x = 180
cos 2x = cos 720
2x = 720
x = 360
Cara kedua
cos 2x = cos 0
2x = 0 (untuk sementara biarkan dalam bentuk 2x)
i) 2x = 0 + k x 360
untuk k = 0 maka 2x = 0 + 0 x 360 sehingga 2x = 0 dan x = 0
untuk k = 1 maka 2x = 0 + 1 x 360 sehingga 2x = 360 dan x = 180
untuk k = 2 maka 2x = 0 + 2 x 360 sehingga 2x = 720 dan x = 360
ii) 2x = - 0 + k x 360 atau 2x = 0 + k x 360
persamaan ii) sama seperti i) maka tak perlu kita lanjutkan lagi
Jadi Himpunan penyelesainnya adalah HP = {0, 180, 360}
3. Tentukan nilai x untuk tan 3x - 1 = 0 dengan 0 < x < 180
Untuk menyelesaiakn soal diatas kita harus olah terlebih dahulu tan 3x -1 = 0 maka kita pindah ruas menjadi tan 3x = 1
Untuk menjawab soal ini kita harus mengetahui tan berapa yang hasilnya adalah 1 ?
yaitu tan 45 apakah hanya tan 45 ? tentu tidak. tan 225 juga hasilnya 1. Apakah ada lagi? iya yaitu tan 405, 585, dan seterusnya
tan 3x = tan 45
3x = 45
x = 45/3
x = 15
tan 3x = tan 225
3x = 225
x = 75
tan 3x = tan 405
3x = 405
x = 135
tan 3x = tan 585
3x = 585
x = 585/3
x = 195 (Tidak memenuhi karena diluar interval)
Sehingga HP = {15, 75, 135}
Cara kedua
tan 3x - 1 = 0
tan 3x = 1
tan 3x = tan 45
3x = 45 (untuk sementara biarkan dulu dalam bentuk 3x)
i) 3x = 45 + k x 180
untuk k = 0 maka 3x = 45 + 0 x 180 sehingga 3x = 45 dan x = 15
untuk k = 1 maka 3x = 45 + 1 x 180 sehingga 3x = 225 dan x = 75
untuk k = 2 maka 3x = 45 + 2 x 180 sehingga 3x = 405 dan x = 135
untuk k = 3 maka 3x = 45 + 3 x 180 sehingga 3x = 585 dan x = 195 (Tidak memenuhi karena diluar interval)
Sehingga HP = {15, 75, 135}
Demikian penjelasan tentang persamaan trigonometri bentuk pertama semoga bermanfaat apabila ada pertanyaan silahkan bisa chat di kolom komentar Terima kasih sudah mampir di matematikakubro.blogspot.com